Researchers Demonstrate First ‘Poor Man’s Qubit’ Probabilistic Computing Hardware

Researchers for the first time have demonstrated hardware for a probabilistic computer, which makes calculations using p-bits, bridging the gap between classical and quantum computing and creating what researchers call "the poor man's qubit." The 8-p-bit hardware used a modified quantum computing algorithm to factorize 945. Probabilistic computers could potentially solve many of the same problems as quantum computers are expected to solve, but could be manufactured based on existing hardware.

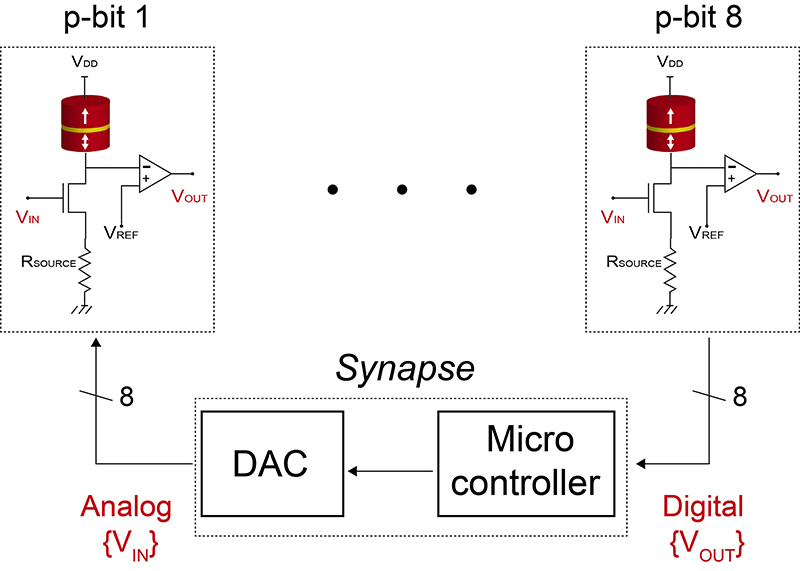
The probabilistic bit, or p-bit, was proposed in 2017 by a research group at Purdue University. Unlike conventional, stable bits, p-bits are stochastic, unstable units: they fluctuate in time between 0 and 1. In other words, they evaluate to 0 (or 1) with a certain probability. They can then be interconnected to implement Boolean functions. Another unique property is that they are invertible. When operating as invertible logic, the output (instead of the input) is provided, and the network will fluctuate between all possible inputs that are consistent with said output. For example, a multiplier in inverted mode functions as a factorizer.

Invertible logic could be seen as one example that digital computers have their limits. Alternative computing schemes could potentially address certain classes of problem sets that conventional computers struggle with. Most notably, in quantum computing a qubit represents a quantum superposition of 0 and 1, and is expected to perform tasks such as optimization, sampling and inference efficiently.

However, quantum computing has several drawbacks. For example, a quantum computer relies on the evolution of what is called a quantum coherence, which can be disturbed by the environment. This causes quantum decoherence, or in other words, loss of information. Another disadvantage is that so far they have to operate at cryogenic temperatures.

Probabilistic computing does not face those challenges, by virtue of being a classical entity that is electrically connected and can operate at room temperature. The researchers say that a subset of problems that can be solved with qubits can also be solved with p-bit, saying that it is the “poor man’s qubit.”

The device that the researchers built is based on magnetoresistive RAM or MRAM (which for example Intel earlier this year said it could mass produce). Such a device uses the orientation of (tiny) magnets to alter the resistance, to represent 1 or 0. Tohoku University researchers in Japan then modified the MRAM to make it intentionally unstable, to facilitate the fluctuations of p-bits. This was combined with a transistor to control the fluctuations.

To build a functional probabilistic computer, eight of these resulting three-terminal p-bit units were then interconnected. And to demonstrate its working, "a modified adiabatic quantum computing algorithm that implements three- and four-body interactions" was used to factorize integers up to 945.

Although the hardware is not yet solving any problems out of reach for classical computers (as is now being attempted in quantum computing), the researchers note that it is performing a function for which thousands of transistors would have been needed:

“On a chip, this circuit would take up the same area as a transistor, but perform a function that would have taken thousands of transistors to perform. It also operates in a manner that could speed up calculation through the parallel operation of a large number of p-bits,” said Ahmed Zeeshan Pervaiz, a Ph.D. student in electrical and computer engineering at Purdue.

The researchers are aiming to scale up the number of p-bits to solve more advanced problems. The paper was published in Nature on 18 September.

Probabilistic computing has already garnered interest towards commercialization. In May 2018, Intel CTO Michael Mayberry announced that Intel increased its probabilistic computing investment and established the ‘Intel Strategic Research Alliance for Probabilistic Computing.’ Intel sees deep learning (AI) as an important application for probabilistic computing. Although in an interview, he pointed out that there are multiple forms of probabilistic computing.