Video Guide Part 3: Video Formats and Compression Methods
Discrete Cosine Transformation (no Data Loss)
Figure 2 shows a section of the side of the car and its headlight as an 8x8 block. This block is assigned to a color value matrix that is used for the discrete cosine transformation (DCT). DCT suppresses highly frequent image parts that aren't apparent to the human eye. DCT is based on Fourier transformations that present any signal as merged (superimposed) sine signals of different frequencies and amplitudes. The Fourier transformation yields frequency and amplitude distribution values from the location of pixel values in an image. This means that large, regular areas in the image are then represented more in the lower frequency parts, whereas finer details are in the higher range. In our concrete example, DCT transforms the displayed 8x8 macro block into an 8x8 coefficient matrix. The value in the upper left corner of the coefficient matrix contains the lowest frequency parts. This coefficient at location 0,0 is normally referred to as the DC coefficient, whereas the remaining 63 coefficients are termed AC coefficients (AC = Amplitude Coefficient). As there is normally a solid relationship between the DC coefficients of two subsequent 8x8 blocks, the DC coefficient is encoded as the difference to the predecessor. The remaining 63 AC coefficients are sorted according to a set pattern.
DCT concentrates the signal energy of a block in the lowest coefficients, especially in the DC coefficient. The higher AC coefficients are normally 0 or almost 0, because the main part of the visual information of an image lies in a continuously distributed range of values in the lower frequency area. Edges normally only constitute a small part of an image. After the discrete transformation, the coefficients are quantized in order to attain an additional compression improvement.
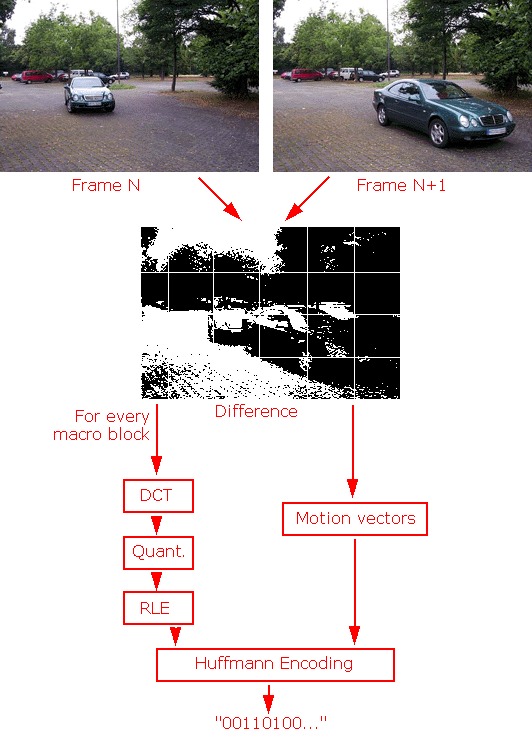
Figure 4: Principle flow of MPEG compression. MPEG-1 reduces the original data volume to about 1:35.
Get Tom's Hardware's best news and in-depth reviews, straight to your inbox.
Current page: Discrete Cosine Transformation (no Data Loss)
Prev Page Subdivision Into Macro Blocks Next Page Quantizing (high Data Loss)