Data-Encoding: Run Length Limited Encoding And Coding Scheme Comparisons
Run Length Limited Encoding
Today’s most popular encoding scheme for hard disks, called Run Length Limited, packs up to twice the information on a given disk than MFM does and three times as much information as FM. In RLL encoding, the drive combines groups of bits into a unit to generate specific patterns of flux reversals. Because the clock and data signals are combined in these patterns, the clock rate can be further increased while maintaining the same basic distance between the flux transitions on the storage medium.
IBM invented RLL encoding and first used the method in many of its mainframe disk drives. During the late 1980s, the PC hard disk industry began using RLL encoding schemes to increase the storage capabilities of PC hard disks. Today, virtually every drive on the market uses some form of RLL encoding.
Instead of encoding a single bit, RLL typically encodes a group of data bits at a time. The term Run Length Limited is derived from the two primary specifications of these codes, which are the minimum number (the run length) and maximum number (the run limit) of transition cells allowed between two actual flux transitions. Several variations of the scheme are achieved by changing the length and limit parameters, but only two have achieved real popularity: RLL 2,7 and RLL 1,7.
You can even express FM and MFM encoding as a form of RLL. FM can be called RLL 0,1 because as few as zero and as many as one transition cells separate two flux transitions. MFM can be called RLL 1,3 because as few as one and as many as three transition cells separate two flux transitions. (Although these codes can be expressed as variations of RLL form, it is not common to do so.)
RLL 2,7 was initially the most popular RLL variation because it offers a high-density ratio with a transition detection window that is the same relative size as that in MFM. This method provides high storage density and fairly good reliability. In high-capacity drives, however, RLL 2,7 did not prove to be reliable enough. Most of today’s highest capacity drives use RLL 1,7 encoding, which offers a density ratio 1.27 times that of MFM and a larger transition detection window relative to MFM. Because of the larger relative timing window or cell size within which a transition can be detected, RLL 1,7 is a more forgiving and more reliable code, which is important when media and head technology are being pushed to their limits.
Another little-used RLL variation called RLL 3,9—sometimes also called Advanced RLL (ARLL)—allows an even higher density ratio than RLL 2,7. Unfortunately, reliability suffered too greatly under the RLL 3,9 scheme; the method was used by only a few now-obsolete controllers and has all but disappeared.
Understanding how RLL codes work is difficult without looking at an example. Within a given RLL variation (such as RLL 2,7 or 1,7), you can construct many flux transition encoding tables to demonstrate how particular groups of bits are encoded into flux transitions.
In the conversion table shown below, specific groups of data that are 2, 3, and 4 bits long are translated into strings of flux transitions 4, 6, and 8 transition cells long, respectively. The selected transitions for a particular bit sequence are designed to ensure that flux transitions do not occur too closely together or too far apart.
| RLL 2,7 Data-to-Flux Transition Encoding | |
|---|---|
| Data Bit Values | Flux Encoding |
| 10 | NTNN |
| 11 | TNNN |
| 000 | NNNTNN |
| 010 | TNNTNN |
| 011 | NNTNNN |
| 0010 | NNTNNTNN |
| 0011 | NNNNTNNN |
| T = Flux transition, N = No flux transition |
Limiting how close two flux transitions can be is necessary because of the fixed resolution capabilities of the head and storage medium. Limiting how far apart two flux transitions can be ensures that the clocks in the devices remain in sync.
In studying the table above, you might think that encoding a byte value such as 00000001b would be impossible because no combinations of data bit groups fit this byte. Encoding this type of byte is not a problem, however, because the controller does not transmit individual bytes; instead, the controller sends whole sectors, making encoding such a byte possible by including some of the bits in the following byte. The only real problem occurs in the last byte of a sector if additional bits are necessary to complete the final group sequence. In these cases, the endec in the controller adds excess bits to the end of the last byte. These excess bits are then truncated during any reads so the controller always decodes the last byte correctly.
Encoding Scheme Comparisons
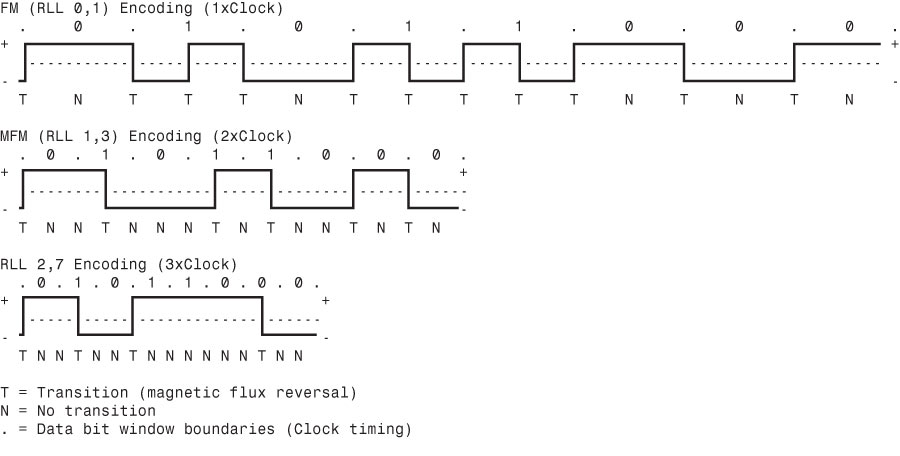
The figure below shows an example of the waveform written to store the ASCII character X on a hard disk drive by using three encoding schemes.
In each of these encoding scheme examples, the top line shows the individual data bits (01011000b, for example) in their bit cells separated in time by the clock signal, which is shown as a period (.). Below that line is the actual write waveform, showing the positive and negative voltages as well as head voltage transitions that result in the recording of flux transitions. The bottom line shows the transition cells, with T representing a transition cell that contains a flux transition and N representing a transition cell that is empty.
The FM encoding example shown in the image above is easy to explain. Each bit cell has two transition cells: one for the clock information and one for the data. All the clock transition cells contain flux transitions, and the data transition cells contain a flux transition only if the data is a 1 bit. No transition is present when the data is a 0 bit. Starting from the left, the first data bit is 0, which decodes as a flux transition pattern of TN. The next bit is a 1, which decodes as TT. The next bit is 0, which decodes as TN, and so on.
The MFM encoding scheme also has clock and data transition cells for each data bit to be recorded. As you can see, however, the clock transition cells carry a flux transition only when a 0 bit is stored after another 0 bit. Starting from the left, the first bit is a 0, and the preceding bit is unknown (assume 0), so the flux transition pattern is TN for that bit. The next bit is a 1, which always decodes to a transition-cell pattern of NT. The next bit is 0, which was preceded by 1, so the pattern stored is NN. By using the table on the previous page, you easily can trace the MFM encoding pattern to the end of the byte. You can see that the minimum and maximum numbers of transition cells between any two flux transitions are one and three, respectively, which explains why MFM encoding can also be called RLL 1,3.
The RLL 2,7 pattern is more difficult to see because it encodes groups of bits rather than individual bits. Starting from the left, the first group that matches the groups listed in the table above is the first three bits, 010. These bits are translated into a flux transition pattern of TNNTNN. The next two bits, 11, are translated as a group to TNNN; and the final group, 000 bits, is translated to NNNTNN to complete the byte. As you can see in this example, no additional bits are needed to finish the last group.
Notice that the minimum and maximum numbers of empty transition cells between any two flux transitions in this example are two and six, although a different example could show a maximum of seven empty transition cells. This is where the RLL 2,7 designation comes from. Because even fewer transitions are recorded than in MFM, the clock rate can be increased to three times that of FM or 1.5 times that of MFM, thus storing more data in the same space. Notice, however, that the resulting write waveform itself looks exactly like a typical FM or MFM waveform in terms of the number and separation of the flux transitions for a given physical portion of the disk. In other words, the physical minimum and maximum distances between any two flux transitions remain the same in all three of these encoding scheme examples.
Partial-Response, Maximum-Likelihood Decoders
Another feature often used in modern hard disk drives involves the disk read circuitry. Read channel circuits using Partial-Response, Maximum-Likelihood (PRML) technology enable disk drive manufacturers to increase the amount of data stored on a disk platter by up to 40%. PRML replaces the standard “detect one peak at a time” approach of traditional analog peak-detect, read/write channels with digital signal processing.
As the data density of hard drives increases, the drive must necessarily record the flux reversals closer together on the medium. This makes reading the data on the disk more difficult because the adjacent magnetic peaks can begin to interfere with each other. PRML modifies the way the drive reads the data from the disk. The controller analyzes the analog data stream it receives from the heads by using digital signal sampling, processing, and detection algorithms (this is the partial response element) and predicts the sequence of bits the data stream is most likely to represent (the maximum likelihood element). PRML technology can take an analog waveform, which might be filled with noise and stray signals, and produce an accurate reading from it.
This might not sound like a very precise method of reading data that must be bit-perfect to be usable, but the aggregate effect of the digital signal processing filters out the noise efficiently enough to enable the drive to place the flux change pulses much more closely together on the platter, thus achieving greater densities. Most drives with capacities of 2 GB or above use PRML technology in their endec circuits.
