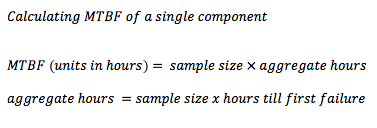MTTF? MTBF? "My Drive Lasts Longer"
I wanted to cover reliability because I've spent some time on a few forums (including those dedicated to storage), noticing that people are discussing MTBF ratings. This deserves a separate page of discussion.
When you look at the data sheet of any drive, you'll notice reliability is expressed in mean time between failures (MTBF) or mean time to failure (MTTF). These two values share the same units. The only difference is that the first assumes you can fix a drive, and in latter, replace it.
| Header Cell - Column 0 | SF-1222 | SF-2141 | SF-2181 | SF-2281 | SF-2282 | SF-1565 | SF-2582 | SF-2682 |
|---|---|---|---|---|---|---|---|---|
| Target Market | Client | Client | Client | Client | Client | Enterprise | Enterprise | Enterprise |
| MTTF (hours) | 2 million | 2 million | 2 million | 2 million | 2 million | 10 million | 10 million | 10 million |
If you look at the mean time to failure (MTTF) of any enterprise controller from SandForce, such as the SF-2582, you'll notice that it's rated at 10 000 000 hours. Yet, the SF-2281 is rated at 2 000 000 hours.
If you do the math, you realize that 10 000 000 hours roughly equals 1140 years. Does this mean you can bequeath an enterprise drive to your tenth-generation progeny?
Not at all. This rating is based on probability. There are many ways to calculate MTBF, but here is one example. Let's say SandForce had 2000 drives based on the SF-2582 in its qualification lab. If you were to turn on all of these SSDs at the same time and start the clock, every passing hour would equal 2000 hours of drives running. For the sake of this example, let's assume the first SSD fails after 2000 hours (~82 days). You would stop the clock the moment the first drive failed and the MTBF would be calculated based on the number of drives originally set up. Because only one drive out of 2000 failed after 2000 hours of use, the MTBF would be four million hours.
The problem with this type of math is that it is hardly considers advanced statistics or stochastic math. For all we know, the entire batch of 2000 drives could have failed five minutes after we stopped the clock. This is why MTBF can be an inflated number (depends on the math used).
While the math may seem a bit odd, this relates to the MTBF rating you see on a drive. For example, Corsair’s Force SDDs use the same SF-1222 seen on OCZ's Vertex 2. Yet, Force drives are rated at 1.5 million to the 2 million hours for Vertex 2. This occurs because the MTBF rating of a drive is based on a sum probability. There are many components that go into making a drive: memory, buck converters, controllers, resistors, and so on. Even though the SF-1222 is rated for 2 million hours, the parts that Corsair is using collectively add up to 1.5 million. Since any system is only as strong as its weakest link, this results in a lower MTBF rating. OCZ claims a higher MTBF because the rating it gives to the parts other than the SandForce controller exceed 2 million hours. Hence, OCZ publishes the reliability rate of the controller as that of the drive.
We point this out because MTBF is not a meaningful way for us to measure how long a drive will last. At the end of the day, it would be incorrect to compare the durability of two different drives simply using the MTBF rating, even if they use the same controller (like the Force and Vertex 2). If you love math, you've already come to the realization that this number can be easily manipulated. The fastest way is to simply increase the number of drives being tested. Double the drives, double the MTBF. Let's put aside the flaw in this approach to calculating MTBF for a moment. Without knowing how many drivers were originally tested, you can't determine how long a single drive might last. Remember this when you are shopping for drives, be it disk or solid state. (If you like academia as much as I do, I recommend reading a paper written by Bianca Schroeder and Garth Gibson for more information. Eduardo Pinheiro, Wolf-Dietrich Weber and Luiz Andr´ Barroso at Google Research have also written a great paper that explores reliability of consumer drives.)
