ARM will be adding BFloat16 support in the next revision of the ARMv8-A architecture under its Project Trillium ML platform. It marks a new major milestone in the widespread adoption of the young data format that is taking the deep learning community by storm. In this article, we’ll dive into the origins and benefits of the format.
Number Formats
It might seem obvious, but one of the fundamental problems you would encounter if you would want to build a computer chip from scratch follows: how do you represent numbers? For integers, the solution is simple enough: use the binary equivalent of the decimal number. (We’ll ignore negative numbers, for which a slightly more elaborate scheme was devised to make computation in hardware easier.) Rational numbers, never mind irrational numbers, need a bit more care, however.
The way to go is to use a (binary) scientific representation, in computer science called floating-point. In scientific notation, a number is represented as a rational number – called the mantissa – followed by a multiplication of this mantissa to the base raised to some exponent. As one caveat, the mantissa contains only one digit before the point, so the first digit in binary scientific notation is always a 1, so it is actually not stored by a computer. An example is 1.11 * 21111. Its value is 1.75 * 215 or 57,344. The mantissa evaluates to 1.75 because the first digit after the point represents a value of 0.5, the second digit 0.25, etc. So the binary 1.101 equals 1.625 in decimal.
In summary, such a number thus contains three pieces of information: its sign, its mantissa (which itself can be positive or negative) and the exponent. To make matters simple, IEEE has standardized several of these floating-point number formats for computers, of which binary32 (or FP32) and binary64 (or FP64) are most commonly used. The number refers to the total amount of digits that are used to represent the number, with most digits being allocated to the mantissa since that provides higher precision. They are also called single-precision (SP) and double-precision (DP). As mentioned earlier, the first digit of the mantissa is not contained in the format since it is always a 1.
When talking about the performance of a chip, the parlance used is floating-point operations per second or FLOPS. This would normally refer to single precision. In high performance computing (HPC), such as the classic TOP500 list, the number looked at is double-precision performance. However, for mobile graphics, and even more recently for deep learning especially, half-precision (FP16) has also become fashionable. Nvidia recognized this trend early on (possibly aided by its mobile aspirations at the time) and introduced half-precision support in Maxwell in 2014 at twice the throughput (FLOPS) of FP32. Since it is a smaller number format, the precision and range are reduced, but for deep neural networks, it turned out to be a feasible trade-off for more performance.
BFloat16
Of course, how the bits are split between the mantissa and the exponent can be freely chosen, in principle. More bits for the exponent means a much wider dynamic range of numbers that can be represented, both larger and smaller, whereas more bits for the mantissa will increase the accuracy of the representation. The latter is usually preferred. As an example, to approximate pi using floating-point representation as closely as possible, you would want to use most bits for the mantissa.
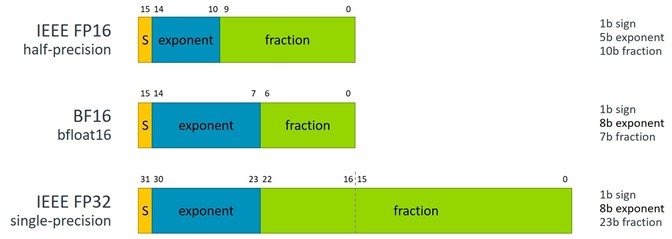
This is why IEEE standards are handy, to standardize this division between mantissa and exponent bits (and also for handling exceptions such as rounding, overflow and underflow consistently across hardware). Despite SP having twice as many bits (16 more), only three of them were given to the exponent, although that does increase the maximum value greatly from ~65,000 to ~1038. The machine precision going from FP16 to FP32 is improved by a factor of ~10,000. The image below shows the single and half-precision formats, and also the new bfloat16 format.
Bfloat16 differs from FP16 exactly in this regards; how the bits are allocated between the mantissa and the exponent. In essence, bfloat16 is just FP32, but drastically cuts down on the precision (mantissa) to fit in the 16 bits. In other words, it is (the dynamic range of) FP32 with 16 bit of mantissa (precision) removed. Or compared to FP16, it gains three bits in the exponent in exchange for three mantissa bits.
A question that naturally arises now, though, why bother with bfloat16 when FP16 already exists? For starters, since it is just a truncated FP32, it does make switching or converting to the format quite easy. Also, while FP16 does improve throughput, it is not a free lunch since its range is greatly reduced. So at best, it takes extra time to make the model suitable for FP16, but possibly also at the cost of getting inferior results. It turned out that throwing away 16 mantissa bits from FP32 does not meaningfully alter the behavior of FP32, making bfloat16 pretty much a drop-in replacement of FP32 with the throughput benefits of FP16.
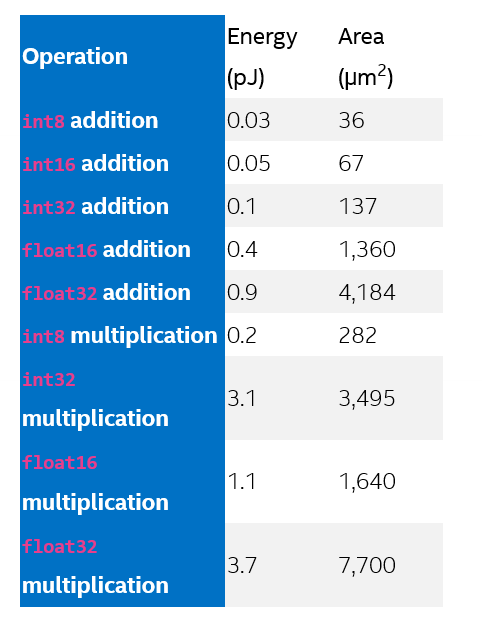
This is not all. The main reason in favor of FP16 is hardware cost – perhaps surprisingly since both are 16-bit formats. As Google explained in a recent blog post, hardware area (number of transistors) scales roughly with the square of the mantissa width. So having just three fewer mantissa bits (7 instead of 10) means that a bfloat16 multiplier takes up about half the area of a conventional FP16 unit. Compared to an FP32 multiplier, its size is eight times smaller, with an equivalent reduction in power consumption as well. Or conversely, within the same silicon area more useful hardware can be put to achieve higher performance.
Lastly, a benefit that is true for all lower precision formats is that it saves memory and bandwidth. Since a value takes up only half the space of FP32, for instance 16GB of memory would suddenly feel more like 32GB by moving to bfloat16. This allows to train deeper and wider models. Additionally, the lower memory footprint also improves speed for memory bandwidth-bound operations.
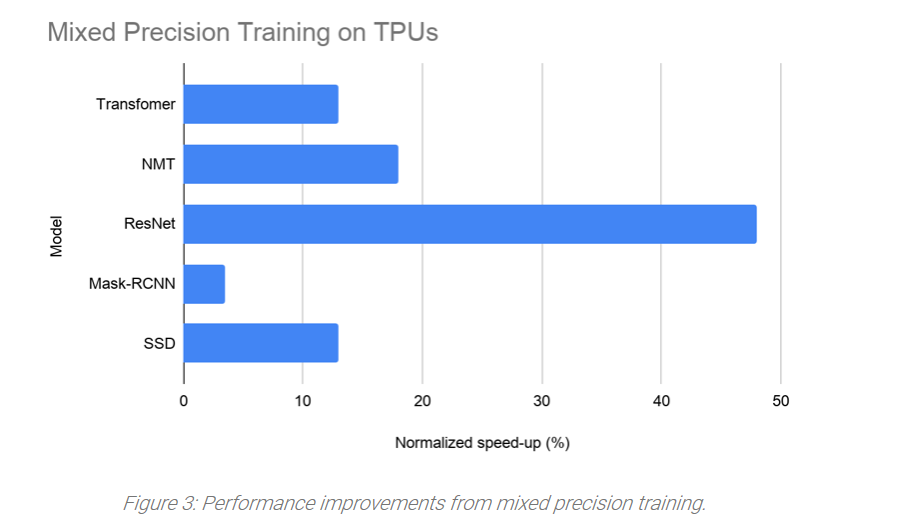
Google reported a geometric mean training speed-up of 13.9% using bfloat16 mixed precision, over several Cloud TPU reference models.
Flexpoint Defeated: The Road to Widespread Adoption
Bfloat16 is called Brain Floating Point Format in full (or BF16 in short), as it is named after the Google Brain research group where it was conceived. As Jeff Dean, Senior Fellow of Google AI, explained in a series of Twitter posts, Google started using the format since the early days of TensorFlow. More specifically, it was supported in hardware since the second version of its Tensor Processing Units (TPUs), the TPU v2 in 2017. But the company didn’t really start to openly talk about it until Google I/O in May 2018 (around 26:00).
Also in May 2018, Intel held its inaugural AI DevCon, where it provided for the first time some performance data on its 28nm Lake Crest deep learning processor and announced Spring Crest as a successor on 16nm and the first high volume Nervana product to launch in late 2019. (Intel also hinted for the first time it was working on an inference chip.)
Lake Crest was the neural network processor (NNP) Intel inherited from acquiring Nervana in the fall of 2016, after which it announced its comprehensive AI strategy and forming its AI Products Group another few months later. One of the innovations Nervana touted for Lake Crest – aside from being a full-fledged deep learning processor instead of a repurposed GPU – was that it used a new optimized numeric data format called Flexpoint (not to be confused with Intel FPGAs’ HyperFlex architecture) that was meant to deliver increased compute density.
Unlike bfloat16, Flexpoint was conceived from the insight that fixed point (i.e., integer) hardware consumes fewer transistors (and energy) than floating point hardware, as Intel explained in an in-depth 2017 blog post. In one table, Intel showed that an integer multiplier costs less than half the area of a floating point multiplier of the same number of bits. Though less relevant, the difference is even larger for addition: while an integer adder scales linearly with the number of bits, a floating point adder scales quadratically, resulting in vast differences in area.
So the idea behind Flexpoint is to make integer arithmetic work for deep learning. Flexpoint is actually a tensorial numerical format. The elements of a Flexpoint tensor are (16-bit) integers, but they have a shared (5-bit) exponent whose storage and communication can be amortized over the whole tensor, making the exponent negligible in cost. In full, the format can be denoted as flex16+5. The common exponent in a tensor isn’t completely free, however, as it does introduce some exponent management complexity, for which Nervana introduced a management algorithm called Autoflex. Intel concluded: “Strictly speaking, it is not a mere numerical format, but a data structure wrapping around an integer tensor with associated adaptive exponent management algorithms.”
In essence then, around 2017 there were two upcoming, competing 16-bit training methodologies that each claimed to provide ‘numerical parity’ to 32-bit training, but with more efficient 16-bit formats. Bfloat16 improved upon FP16 by exchanging mantissa bits for exponent bits, while Flexpoint improved upon FP16 by moving to integer arithmetic (with some marginal exponent management overhead). Interestingly enough, flex16+5 actually has higher precision than FP16 (or bfloat16) because it has 16-bit mantissas (due to the separate 5-bit exponent).
However, by the time Intel formally introduced Spring Crest at the AI DevCon in 2018, all notions of Flexpoint had disappeared. Naveen Rao, Nervana co-founder and SVP of the AI Products Group, instead announced that the product would support bfloat16. This was further strengthened when a few months later Naveen Shenoy, SVP of Intel’s Data Center Group, announced that Intel would go all-in on bfloat16 and introduce it across the company’s portfolio, with Cooper Lake being the first Xeon CPU to support it as new DLBoost feature. In November 2018 Intel released its own bfloat16 hardware numerics definition whitepaper (PDF) for integrating BF16 units in Intel Architecture, definitely vindicating Google’s Brain Floating Point Format.
It remains an open question why the company went overboard with BF16, as Intel never explained why Flexpoint fell by the wayside. Intel had touted that there was no extra software engineering needed to move from FP32 to flex16+5, making it a drop-in replacement just like BF16. Intel may have simply decided that a numeric format battle was not worth it, and chose to accept – and even push – BF16 as the standard deep learning training format. After all, both proposals claimed about the same ~50% reduction in area compared to FP16.
The NNP-T and Xeon Scalable processors likely won’t be the only products from Intel to support BF16. While it not clear yet if Ice Lake will feature the format, Intel’s 10nm Agilex FPGAs also have hardened support for it.
One other question is also left open that is probably easier asked for Flexpoint than for BF16: why (stop at) 16 bits? After all, moderate precision is making big strides in inference. For example, Google’s TPUv1 supported just INT8. Intel answered this by noting that low precision remains a challenge for training for several reasons. So for now, bfloat16 will become the de facto standard for deep neural network training on non-Nvidia hardware. Although it must be noted that Nvidia does make up the majority of the training market.
ARM Confirms BF16 Commitment
ARM recently announced in a detailed blog that it is also committed to the new format. The instructions that ARM is adding are solely for BF16 multiplication since that is by far the most common computation in neural networks. Specifically, the SVE, AArch64 Neon and AArch32 Neon SIMD instruction sets will each gain the four new instructions. (SVE is an ARMv8 extension complementary to Neon, and it allows for vector lengths to scale from 128 to 2048 bits.) The instructions accept BF16 inputs, but they accumulate into FP32, just like other BF16 implementations. One instruction allows for converting to BF16.
ARM also explained some of the nuances concerning numeric behaviors (rounding behavior) of BF16. It noted that different architectures and software libraries had adopted slightly different mechanics for rounding, and ARM too has not followed FP32 rigorously and instead introduced some simplifications. However, ARM states that its simplifications have resulted in a 35% or more area – and corresponding power – reduction of such a block. Conversely, ARM says they also permit the reuse of existing FP32 blocks to deliver twice the BF16 throughput (compared to FP32) with only a slight increase in area.
The new instructions fall under ARM’s Project Trillium, its heterogeneous machine learning program. The new BF16 instructions will be included in the next update of the Armv8-A instruction set architecture. Albeit not yet announced, this would be ARMv8.5-A. They should find its way to ARM processors from its partners after that.
Summary
In a quest for ever higher deep learning performance, hardware and software has moved to lower precision number formats to reduce the hardware size of the arithmetic units and increase throughput. Since FP16 posed some challenges because of its reduced value range, Google moved to its self-devised bfloat16 format with the TPUv2 in 2017 as a superior alternative and a drop-in replacement for FP32, all while cutting hardware area in half compared to FP16, or eightfold over FP32. Its appeal is that it is simply a truncated FP32.
Intel, on the other hand, inherited Flexpoint from its Nervana acquisition. It touted the same end-user benefits of FP32 model performance and improved compute density compared to FP16, but employing integer hardware. However, Intel at some point moved forward with pushing BF16 across its portfolio. It has now been announced for the NNP-T accelerators, Xeon Scalable (Cooper Lake for now) and the Agilex FPGAs.
While Nvidia has made no announcements on this front, ARM last week also said that it would support bfloat16 multiplication with several SVE and Neon instructions in the next revision of the ARMv8-A architecture. With that announcement, the two most important CPU architectures are now in the process of receiving hardened BF16 support.
