A Prima Donna on PC: Creative Labs Audigy 2

So What Is 24/ 96 For?

To understand the advantage of sound encoded in 24 bits and sampled at 96 kHz, here is a brief explanation of the way sound is digitized. When an analog sound is digitized, the analog flow is sampled at given intervals. At each of these intervals, the sound level is measured and represented by a numeric value. In CD Audio for instance, 16 bits are allocated for each value, so there are 65,536 values for one measurement (2 to the power of 16). Now, as digitization only accepts integers and not decimals, there will be an error, or, rather, an approximation when the analog signal falls between two integers that can be represented. This error is different for each value represented. The difference between the real value and the digitized one appears as superimposed when played, and is called "quantization noise." However, quantization noise is theoretically 96 dB lower than the maximum quality control parameter, which is infinitesimal compared to most of the inevitable interference observed in digitization. This being so, it would seem pointless to increase the digital resolution in order to decrease quantization noise, yet we shall see later on that this is not just theory.

To ensure there is no over-modulation during digitization, an ADC (Analog-to-Digital Converter) must reserve part of its resolution for what is called "headroom." And this is where the 24 bit system has the edge, because it retains most of its resolution (20 bits) whereas 16 bit headroom is only 14 bits at the most. And given that 24 bit resolution provides 16.7 million values to represent an analog flow, the quantization noise of a 24 bit converter is theoretically -144 dB, a truly negligible amount of interference.

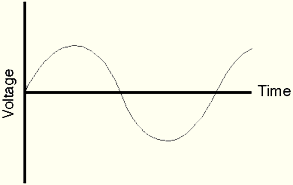
So, the input signal in digitization is like this:

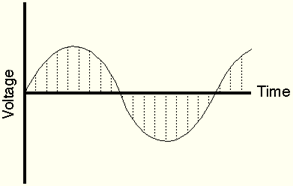
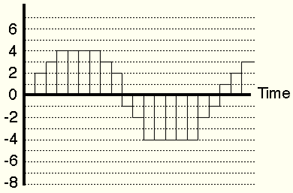
This signal is then broken down into a series of sampling periods:

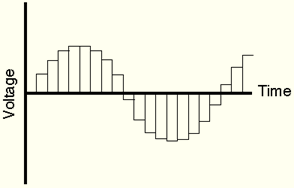
After sampling, the converter eliminates the intermediate signals and rounds off those found by the sampling rate.

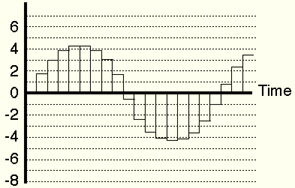
A value is then allocated to each signal; in 16 bits the value ranges from 0 to 16,536, and in 24 bits from 0 to 16,700,000. If a signal has a value that does not match an integer which can be allocated, the converter rounds it up or down to the nearest integer. This method is the source of the errors called quantization.

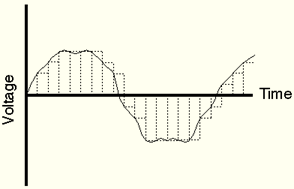
The converter next uses a reconstruction filter to rebuild a curve which is truer to the original than the one above. Note that our example is greatly exaggerated to make the demonstration more clear. After filtering, the curve looks like this:

The main point of this operation is to cut out the high frequencies, these being most inclined to generate errors, so a Low pass filter is applied to cut out sounds above a certain frequency. The fewer errors there are in digitization, the less need there is to cut out high frequencies. So, when 16.7 million values are available for each change in amplitude, it is easier to preserve the fidelity of the high frequencies. According to the Shannon theorem, the highest frequency that can be represented amounts to half the sampling rate. So, if the sampling rate is 44.0 kHz, the highest frequency that can be reached is 22.05 kHz. This cutoff frequency is also called the "Nyquist" frequency.

If the sampling rate is raised to 96 kHz, the Nyquist frequency rises to 48 kHz, making it possible to reproduce a much wider range of high frequencies. But let's not forget a very important detail in this respect: the bandwidth in the best of human hearing never exceeds 20 kHz and is around 17 kHz in adults, though a number of sound buffs believe that increasing the bandwidth beyond what can actually be heard substantially improves perception of sound because of the harmonics created by the sounds beyond the limit. This is known as "residual listening." Scientific experiments on this have never been able to prove once and for all the beneficial effects of residual listening, but we can establish some things about sound resolution and sampling rates:

• If the aim is to digitize, work on, and recreate an analog sound, there is no doubt about the advantage of 24 bits/ 96 kHz. The object of the exercise being to retrieve the original curve in the end, you are more likely to do so if your source base contains as much information as possible. In this instance, a sound "captured" 96,000 times a second and encoded each time on a panel of 16.7 million values is better than one "captured" 44,100 times and encoded on a panel of 65,536 values.

For a more detailed explanation of this subject, we strongly recommend two online files: http://www.tonmeister.ca/main/ and http://www.terratec.de/4G/2496-en.pdf .